電腦基礎概論
概述:
一、產生背景:
十九世紀末,由於科技與工商業的發達,人類活動的項目與範圍,不斷增加與擴大,遂造成一個新的『資訊爆發』時代。再加上人類因時間與空間觀念的改變,對於即時與正確情報的需求也愈感迫切。在這種情況下,大量繁雜之資料需經迅速而正確的處理、傳遞或計算,方能滿足人類真正需求。傳統的人工作業方式只能處理較少量且較無時間性的資料,對於大量且需即時處理的資料,已難以滿足,而其方法亦漸不切實際。歐美國家乃殫精竭慮研究發明了電子計算機(俗稱電腦),以作為快速處理或運算大量資料之工具。
電腦的使用,在人類發展史上應屬第二次工業革命。在第一次工業革命中,人類藉著機械與動力之發明,延伸其工作能力;而第二次電腦的革命中,人類則使用計算機延伸其計算能力。由於積體電路技術日新月異,使電腦硬體價格不斷下降,更助長其推廣使用。不僅改變人類的日常活動,而且改變其思想觀念與組織結構。人類從此更離不開電腦的服侍了。在電腦的協助下,可以用最少的人力、時間與資源,但達到最大的工作效益,對講究勤能補拙、勤儉美德的中國人來,電腦正是實踐這些優良傳統的現代工具。目前電腦已不只是資訊工業產品而已,它是『生活』的一部份,在民眾的生活、行政效率與工商業發展等各方面都發生影響。
在軟體發展方面,過去資訊工業剛萌芽時,電腦硬體的價值佔八成,軟體只占二成;但近手來硬體價格逐年下降,而硬體則因不斷成熟的各種應用軟體的開發上市,使得硬體與軟體的價值逆轉為二比八,而中國人是一個具有高度智慧的民族,最適合發展軟體工業。
二、電腦的定義:
電腦之發展是以計算機Computer為基礎,經過長時間之研究發展而開發出來的一種高性能的資料處理裝置。因此在對電腦下定義之前我們必須先對計算機作個詮述。
2-1 計算機( Computer)
計算機一詞有很多種解釋,而就其基本功能而言,它是一種高性能的作業裝置,能接受資料之輸入,並對這些資料按照適當的程序加以處理後,將其結果輸出。
計算機
┌───┐ ┌──────┐ ┌────┐
│ 輸入 ├────┤ 資料處理 ├───┤ 輸出 │
└───┘ └──────┘ └────┘
2-2 電計算機(Electronic Digital Computer)
電腦(Electronic Brain)
電子計算機(俗稱電腦),係由許多具備不同功能之機械,電子設備所組成的一組機器。而其功能乃是利用輸入設備輸入資料(Data),然後將資料儲存在主儲存體(Main Memory)中然後再依使用者的控制(Control),將這些資料經過運算(Arithmetic)或邏輯分析(Logic ),使其產生有用的資訊(Information)後,經由輸出設備輸出資訊,以供使用者參考。
由於它具備了人腦處理問題的模式,一般人慣常稱呼它為電腦(Electronic Brain)。事實上,不管怎樣,一個是學名,而另一個則是俗名,只不過稱呼的場合罷了。
三、電腦的特性:
在基本上,電腦有下列三項功能:
- 1. 快速且精確的運算能力。
- 2. 強大而有彈性的記憶能力。
- 3. 能回答邏輯思考性的問題。
這三點也正是人腦所缺乏的,所以它與人腦配合起來,可發揮神奇的效果。
四、電腦的應用:
電腦的應用範圍非常廣泛。凡是問題的解決方法與程序能被編寫成程式指令者,都可納入電腦處理。有一點值得注意的是,雖然電腦的功能強大,決算速度甚快,但並不是所有的工作都適宜使用電腦處理。有些工作太過份強調用電腦處理時,其效果反而會適得其反。較適合使電腦的事情大多是資料量龐大,強調正確計算或限時者。
科技之進步,已使過去之夢幻逐一成真,未來『秀才不出門,作遍天下事』之美景,將因『通訊到家 』目標之達成而實現。
(一)一般應用:
- 無人彈奏能自行演奏的鋼琴。
- 坐在家中即能向各中西餐廳點菜的電腦系統。除了點菜之外,其他娛樂方
- 面的信息亦可在家獲得立即的提供。
- 電腦護膚、理髮、定裝及購買衣服之配衣系統。以縮短女人上街的時間。
- 自動考照、換照、補發駕照系統。公路局監理站目前己開始使用此套系統,以縮短考照的時間。
- 休閒觀光資訊系統。要到某一個地方若不能先獲該地的資訊,有時其為不便。電腦的連線即可解決此一問題。學電腦的孩子不會變壞,將來電動玩具回到家裡來後,也比較容易管教了。
- 醫療保健系統。如行政院衛生署及民總院之職業病防治中心,提供職業病與環境之診斷、醫療及追蹤等並提供有關職業、環境因素對健康影響之諮詣服務等。
- 將來專家系統亦可以應用到醫療服務系統上,病人僅需按電腦的所詢問的病徵,即可由電腦獲得有關疾病的名稱及所需之用藥,以取代不耐煩的醫生。
- 學術教育資訊系統。學生與老師間的關係愈來愈緊張,利用電腦教學可以減輕這種顧慮。
- 衣食住行育樂資訊系統。
- 電話系統:影像電話高雄金門間已開放,可直接看到對方,每三分鐘一百元。這對當兵的好男而言未始不是一項福音。中文顥示型無線電叫人系統及大哥大實在方便,但也讓忙的人更加忙碌。整體服務數位網路(IDSN)可利用現有之銅纜提供語音、數據、影像及控制等多樣化之服務。使上述的方便更為顯著,電話恐嚇的案子應愈來愈少了。
- 家庭警報系統:竊盜增多,是目前治安之隱憂,利用電腦的控制與預警,可以使個家的安全更有保障。且其間亦可進行各種控制的工作,以彌補人手之不足。
(二)完整的個人及辦公室資訊管理系統
- 備忘錄:小型的文書處理系統。
- 行程管理/工作計劃/萬年曆/農民曆/鬧鐘:協助查詢過去或安排未來工作上各種約會及計劃。除每日之工作安排之外亦設定每週例行的工作計劃。
- 計算機:提供桌上型計算機之功能,具四則運算、記憶式運算、括弧與邏輯運算功能。
- 名片夾:將名片或客戶資料建立成名片檔,系統自動提供索引功能,以供快速之更新、查詣及列印。
- 資料管理工具:將日常生活上或工作上各種重要資料分類歸檔,以利查詢及更新。可以建立:客戶資料、書籍及剪報資料等管理系統。
- 萬用手冊:提供各種常用之資料庫,可供即時之檢索及查詢,包括:國際電話各國國碼及主要城市之區域號碼,主要家之國定假日。
(三)工商業方面之應用
- 國防科技方面:如工程的設計、摸擬與控制等作業。實際之過程如炸藥生產自動控制系統,運用電腦執行炸藥危險品生產自動控制。彈道設計、測試自動化系統,藉彈道設計、測試自動化系統運用電腦高速計算與分析能力,以找出最佳的參數。光電追蹤指揮自化系統,執行目標搜索、軌跡預測、追蹤及姿態穩定功能。
- 會計、統計方面:如薪資計算、成本分析、實用分析、統計事務...等。其中主要包括總帳會計作業、銀行票據作業及員工薪資作業等。
- 管理方面:生產管理、銷售管理、事務管理、人事管理、庫存管理...等。一般餐飲業、商店、工廠、批發、零售及加工業等之作業程序如貨品作業、客戶廠商、進貨作業、應付帳款、支援作業、庫存進出、銷貨作業及應收帳款等。
- 預測、分析及調查方面:生產預測、銷售預測、投資分析,財務分析,股票分析等。可提供成本分析、買進賣出判斷、價格排名表及券商大勢分析等。
- 金融方面:存放款、匯兌、股市行情分析、保費計算、票據交換...等。
- 教育方面:閱卷、圖書管理、電腦教學、成績統計...等。
- 交通方面:鐵、公路與航空之訂座、公路監理、港灣...等作業。
- 公共行政方面:民意調查、犯罪記錄分析、稅捐計算、選舉..等。
- 醫學方面:病歷管理、藥品管理、病患追蹤...等。
- 日常生活:微電腦控制家庭用品、家用電腦、電動玩具,...等。其他如
- 租屋資訊交換的崔媽媽服務中心、電腦擇偶中心。遊戲程式如電動玩具、三國志、俄羅斯方塊。
- 電傳視訊服務:現有之BBS網路、如電信局之電傳系統、農委會之農
- 情報導系統、勞委會職訓局之企業/職業訓練活動資訊系統,只要加入其系統,各訓練機構提供的課程研討會、演講會、考察團、職業訓練及檢定、兢賽等資訊活動均能從自已的電腦螢上查到。
- 多媒體系統:結合處理不同媒體的能力,包括文字、數據、圖形、靜態畫面、動畫、影像、聲音和特殊音效等,而由電腦微處理器控制做交談式對話的系統產品。
利用電腦影像、音響效果、光碟及中央處理機組成。其功能分:
- 多媒體數位化週邊處理裝置及控制軟體。
- 多媒體處理工作站。
- 多媒體發展系統。
可能用途:簡報系統、展示系統、大型視訊板、影音製作、導覽系統、查詢
系統、教育訓練、銷售促進等等。
- 簡報場合:提昇聲音、影像表現力與訴求力。如達文西、展昭
- 娛樂場合:提昇聲音及影像品質。屬低中層次之產品,以Video Game使用為主。
- 教育訓練場合:提高使用者人機介面品質。
(四)、農業方面之應用:
- 作業分析及系統模擬:農機成本分析、農家記帳系統、農機管理系統、農機修護物料管理系統、豬牛等生長及飼料管理系統。植物生長模擬、穀物乾燥模擬、農產物應力分析、風場流動分析,...
- 自動控制之應用:曳引機駕駛控制、水平控制、耗油量控制、打滑率控制、收穫機損失控制、脫粒筒轉速控制、田間作業速率控制、播種精度控制、插秧間距控制、溫室控制、乾燥機操作控制、農機作業安全之警示。
- 影像處理辨識及光電技術之應用:農漁產品、穀物之顏色選別、大小選別、異物選別、成熟度之辨識。
- 機器人之應用:噴藥作業、水果採摘、花卉之盆栽、高級農作物之選別、植物工廠、協助廢棄物之處理。
- 人工智慧及專家系統之應用:農機元件之製造、牲畜疾病之檢查與診斷、農機故障之診斷、引擎故障之診斷、農作物產量之預估、市場價格之警報等。
- 毛豬拍賣系統:早期毛豬拍賣市場幣端甚多,利用電腦可以自動過磅、買主身份及繳款額度控制、競價過程到成交後之各式報表產生等全部由腦連線控制。台北縣肉品拍賣市場每天要處理數千頭豬隻,平均每六秒即有頭豬成交。
- 其他應用:CAI、協助教學、協助農機試驗、檢查動物發情期、懷孕期、倉儲自動化作業等。
(五)、微電腦之一般應用(套裝軟體)----------------------------------------
- 文書處理、簡報系統、繪畫系統、排版系統PE II、KS2、慧星一號、天蠍星、WORD STAR、MS WORD、WORD PERFECT 達文西、變影 72、DR HALO、PC PAINT、PAINT BRUSH、MAC PAINT、GEM 雅墨、畢昇、漢通、天工、PAGE MAKER
- 速算表、資料庫處理國喬雙子星、LOTUS 1-2-3、EXCELL、 MULTIPLAN、... 慧星二號、DBASE III+、DBASE IV、FOXBASE、RBASE、 ...
- 工程繪圖及製造 AUTOCAD、CADKEY、VERSA CAD、MAC DRAW、...
- 統計及製表 STATGRAPH、SAS、SPSS、MS CHART、ENTERGRAPHICS
- 通訊軟體: PROCOMM、TELIX、CROSSTALK、PCTALK、APPLETALK
討論題目:
1. 什麼是電腦?他的功能如何?
--輸入輸出、大量記憶、快速運算及邏輯運算。
2. 電腦具有之特性:
--有容乃大,容量大佔空間小。
--電光石火,運算速度快。
--孔明神算,精確度高、品質劃一。
--千里一線牽,具備電傳能力。
--恆久忍耐、永不止息,永不疲乏。
3. 電腦的歷史:
--機械時期:1642-1946
--真空管時期:1946-1954 第一代
--電晶體時期:1954-1964 第二代
--積體電路時期:1964--? 第三代
-SSI
-MSI
-LSI
-VLSI 第四代
4. 什麼叫硬體? 什麼叫軟體 ?(韌體?)
--靈魂與軀體
--機體與程式
5. 電腦之基本結構:
--輸入部門
--記憶部門 ─┐
--計算及邏輯部門─┴─中央處理部門
--輸出部門
--控制部門
6. 電腦的分類:
--大型電腦:超級快速電腦
--中型電腦
--小型電腦:迷你級
--微型電腦:個人電腦或家用電腦
7. 中央處理部門:
a. 中央處理機 CPU
--6502、Z80、Z8
--8088、8086
--80286、80386、80486
--68000、68020、68030
b. 唯讀記憶體(ROM)
c. 隨機存取記憶體(RAM)
d. I/O通道
e. 資料、住址及控制用排線
8. 記憶體及資料之儲存
--位元(bit)
--位元組(byte)
--位址(address)
五、電腦的演進:
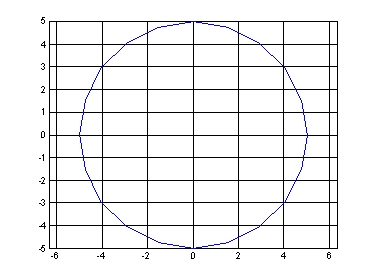 圖1.半徑為5圓心為原點之圓
圖1.半徑為5圓心為原點之圓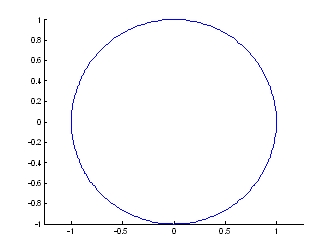 圖2.半徑為預設值1圖心為原點之圓
圖2.半徑為預設值1圖心為原點之圓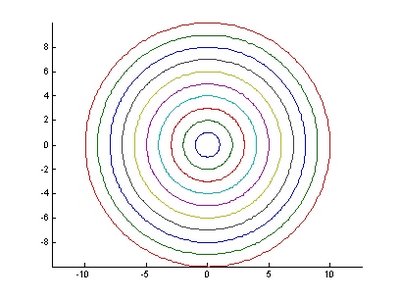 圖3.同心圓
圖3.同心圓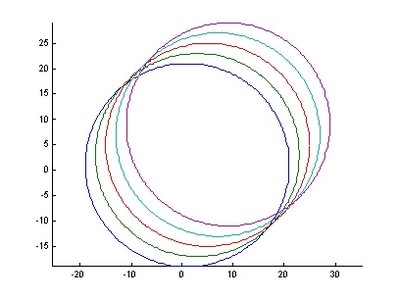 圖4.同心圓不同圓心位置
圖4.同心圓不同圓心位置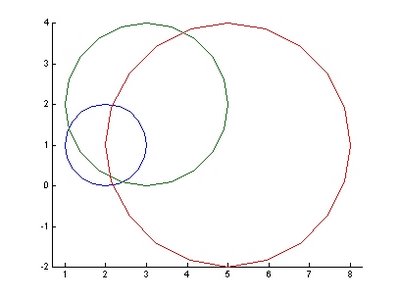 圖5.不同半徑及圖心下之各圓
圖5.不同半徑及圖心下之各圓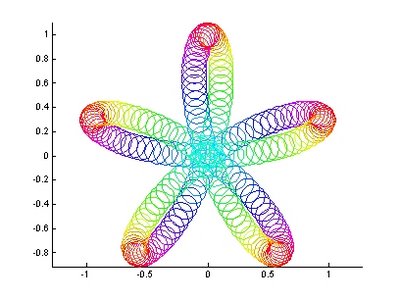 圖6.固定半徑但變化圖心位置下之各圓
圖6.固定半徑但變化圖心位置下之各圓 圖7.利用網格製作同心圓
圖7.利用網格製作同心圓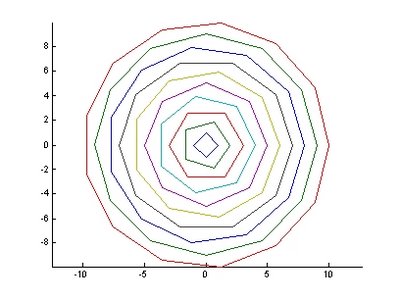 圖8.利用圓周之點數繪製不同之正多邊形
圖8.利用圓周之點數繪製不同之正多邊形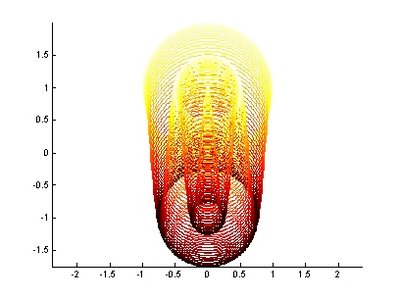 圖9.變化半徑及垂直圓心座標之情形
圖9.變化半徑及垂直圓心座標之情形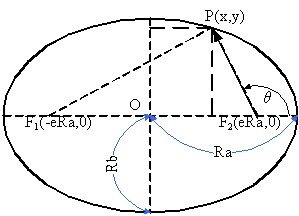 圖10.橢園曲線之形成
圖10.橢園曲線之形成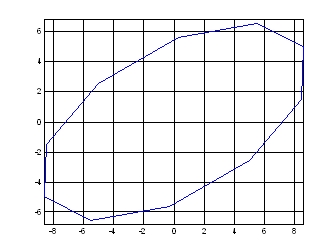 圖11.橢圓曲線之形成
圖11.橢圓曲線之形成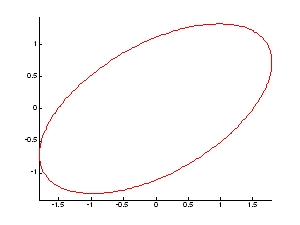 圖12 具有傾斜角度之ellipse 圓
圖12 具有傾斜角度之ellipse 圓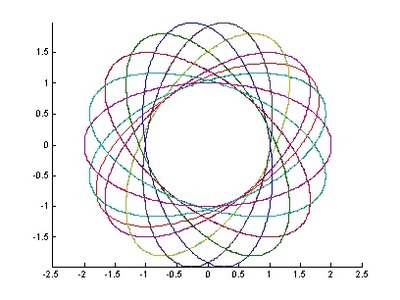 圖13.橢圓產生不同角度旋轉時之變化
圖13.橢圓產生不同角度旋轉時之變化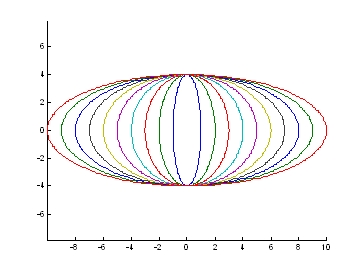 圖14.短徑不變,橢圓產生不同長徑時之變化
圖14.短徑不變,橢圓產生不同長徑時之變化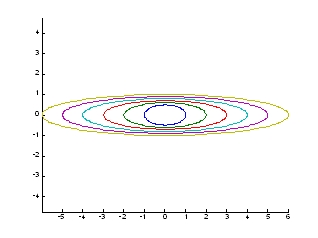 圖15.橢圓長短徑同時變化
圖15.橢圓長短徑同時變化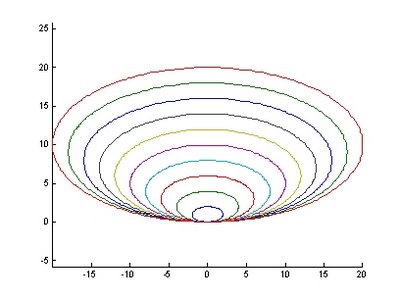 圖16.橢圓產生不同長徑時之變化
圖16.橢圓產生不同長徑時之變化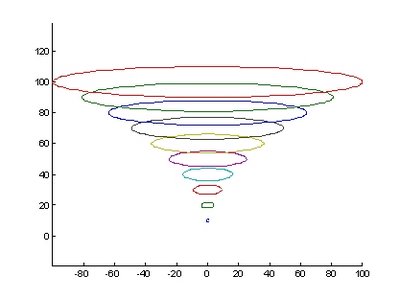 圖17.橢圓產生不同長徑時之變化
圖17.橢圓產生不同長徑時之變化