橢圓繪圖程式之應用
依據公式1.4,橢圓之座標點可用ellipsexy()這項函數求得,其輸入參數包括半長短軸Ra、Rb,中心座標(x0,y0),迴轉角度ang及點數 nn等。其座標值則儲存在coords中,可以直接用來繪圖。其程式之內容如下:
function [coords] = ellipsexy(ra,rb,x0,y0,ang,nn)
% function [coords] = ellipsexy(ra,rb,x0,y0,ang,nn)
% This function draws a ellipse with a long radius ra,
% and short radius rb at the center (x0,y0)
% The inputs:
% ra, rb = long & short radii of the ellipse
% x0, y0= coordinates of the ellipse center
% nn = number of drawing points
% ang = angle of the long axis, in radians
% coords(nn,1-2)= vectors to store the coordinates
% Example: ellixy(10,0,0,10)
jj=0:2*pi/nn:2*pi;
coords=[ra*cos(ang)*cos(jj)-rb*sin(ang)*sin(jj)+x0;...
ra*sin(ang)*cos(jj)+rb*cos(ang)*sin(jj)+y0];
本程式ellipsexy()並未有繪線之功能,可以配合plot()或linke()等繪線函數為之。仍採用line 的功能,逐點連線繪製。由於連線係以直線表示,因此必須在適當的點數下才能繪出近似橢圓形,故點數也相當重要。下面之實例中,點數僅10點,故其橢圓未能成形,可以比較其所繪出之圖形。
實例:半長短軸分別為10、5,中心座標為原點,長軸迴轉30度,試繪出其外形。
>> coord=ellipsexy(10,5,0,0,pi/6,10)
coord =
Columns 1 through 8
8.6603 5.5368 0.2985 -5.0538 -8.4758 -8.6603 -5.5368 -0.2985
5.0000 6.5903 5.6633 2.5731 -1.4999 -5.0000 -6.5903 -5.6633
Columns 9 through 11
5.0538 8.4758 8.6603
-2.5731 1.4999 5.0000
>> plot(coord(1,:),coord(2,:))
>> axis equal;grid on
具有繪製橢圓功能之函數為ellipse0()。可以多重繪製各種橢圓。其程式內容如後,主程式並呼叫副程式ellipsexy(),後者可以另行建檔,或附於呼叫程式之後。其相關參數如後:
- ra, rb:橢圓之半長短軸,可為列矩陣,若為列矩陣時,代表可同時繪製許多橢圓,原則上兩陣列之大小應相同,若其中一個為常數(即為1x1陣列),程式會自動調整與其他一項目同。
- ang:長軸之傾斜角,以度度表示。可為列矩陣,若與ra或rb之大小相同,則會在各中心點處繪製對應之單一橢圓。
- x0,y0:橢圓之中心座標,可為矩陣,若為矩陣時,代表可同時繪製許多不同圓心位置之橢圓。
- C:橢圓線之顏色,可為RGB之三組數值,是為行矩陣。亦可用代碼表示。如['r';'b';'k'...]。注意為使其形成行矩陣,中間必須用分號隔開。
- Nb: 繪ellipse 圓時所用之點數。預設值為300。
其他參數配合使用原則:
- 若ra 為單一項,x0,y0 為向量矩陣,則會繪製向量矩陣數之橢 圓。若x0,y0 為單一項,則會繪製同心橢圓。
- ra 為向量矩陣,則會繪製同一橢圓心之不同半徑向量矩陣數之橢圓。
- ra 均為同大小之矩陣向量,則會繪製數目相同之橢圓。 若x0,y0 與ra 均為不同大小之矩陣,則會繪製總數為兩矩陣數目之乘積。
- 實例:繪製一個傾斜某30角度之橢圓。
>> ellipse0(2,1,0,0,30,'r')
ans = 152.0020
實例:在相同半長短軸及中心點下,可以變化角度,產生旋轉之橢圓群:
>> ellipse0(2,1,0,0,0:20:360)
ans =
Columns 1 through 8
160.0020 161.0020 162.0020 163.0020 164.0020 165.0020 166.0020 167.0020
Columns 9 through 16
168.0020 169.0020 170.0020 171.0020 172.0020 173.0020 174.0020 175.0020
Columns 17 through 19
176.0020 177.0020 178.0020
實例:若半短軸維持不變(可以輸入單一值),配合半長軸進行變化。
>> ellipse0(1:10,4,0,0)
ans =
Columns 1 through 8
152.0024 156.0024 157.0024 158.0024 159.0024 160.0024 161.0024 162.0024
Columns 9 through 10
163.0024 164.0024
實例:同時變化半長短軸,其他維持不變。
>> ellipse0(1:6,0.5:0.1:1.0)
ans = 152.0026 156.0026 157.0026 158.0026 159.0026 160.0026
實例:變化半長短軸,也變化Y軸之高度。
>> ellipse0([1:10]*2,1:10,0,1:10)
ans =
152.0037 156.0037 157.0037 158.0037 159.0037 160.0037
161.0037 162.0037 163.0037 164.0037
實例:曲線變化半長短軸,也變化Y軸之高度。
>>ellipse0([1:10].^2,1:10,0,[1:10]*10);
程式內容:
function h=ellipse0(ra,rb,x0,y0,ang,C,Nb)
% h=ellipse0(ra,rb,ang,x0,y0,C,Nb)
% Adding ellipse to the current plot
% Variables:
% ra,rb:longitudinal & horizontal axes of a ellipse, scalar or matrix.
% ang: angle the ellipse inclines, in deg.
% x0,y0: Centers of the ellipses, a scalar or row matrix
% C:line colors, a string ('r','b','k'...),or RGB values in column
% Nb:No. of drawing points, a scalar or row matrix(default=300)
% h:handles to the ellipse
% Rules:
% 1. ra,rb= matrix, (x0,y0)=a scalar:Multiple co-centered ellipes
% 2. ra,rb= scalar, (x0,y0)=row matrix: ellipse with ra & rb at each center
% 3. ra,rb,(x0,y0)=same length row matrix: ellipse with coresponding r at
% cooresponding center
% 4. ra,rb & (x0,y0)=different-length row matrix: multiple ellipses with
% different pairs of ra & rb at each center
% 5. ra, rb should have same size
% Examples: (execute the commands "clf;" first)
%% Example 0: ellipse0
% ellipse0(2,1,0,0,0:10:360);
% clf;ellipse0(3,1,[0 2 5],[0 1 4],0:10:360)
% ellipse0(ra,rb,ang,x0,y0,C,Nb), Nb specifies the number of points
% ellipse(1,2,pi/8,1,1,'r')
% author: Din-sue Fon. Bime, NTU, Date:November 18, 2004
axis equal;
if nargin <7,Nb=300;end
if nargin <6,C=get(gca,'colororder');end
if nargin <5,ang=0;end
if nargin <4,y0=0;end
if nargin <3,x0=0;end
if nargin <2,rb=1;end
if nargin <1,ra=2;end
% change the matrices into one row
x0=x0(:);y0=y0(:);ra=ra(:);rb=rb(:);ang=ang(:)*pi/180;
nr=length(ra);nx=length(x0);
if length(rb)>nr&nr==1,ra=ones(length(rb),1)*ra;end;
if nr>length(rb)&length(rb)==1,rb=ones(nr,1)*rb;end;
if length(y0)>nx&nx==1,x0=ones(length(y0),1)*x0;end;
if nx>length(y0)&length(y0)==1,y0=ones(nx,1)*y0;end;
nr=length(ra);nx=length(x0);nnb=length(Nb);nang=length(ang);
if length(y0)~=nx|length(rb)~=nr,
error('The lengths of ra & rb should have same size!');
return;
end
if isstr(C),C=C(:);end;
for k=1:nx,
if nx==nr,
for n=1:nang
coords=ellipsexy(ra(k),rb(k),x0(k),y0(k),ang(n),...
Nb(rem(k-1,nnb)+1)+1);
h(k,n)=line(coords(1,:),coords(2,:));
set(h(k,n),'color',C(rem(k*n-1,size(C,1))+1,:));
end
else
for m=1:nr
for n=1:nang
coords=ellipsexy(ra(m),rb(m),x0(k),y0(k),ang(n),...
Nb(rem(m-1,nnb)+1)+1);
h(k,m)=line(coords(1,:),coords(2,:));
set(h(k,m),'color',C(rem(k*m*n-1,size(C,1))+1,:));
end
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [coords] = ellipsexy(ra,rb,x0,y0,ang,nn)
% function [coords] = ellipsexy(ra,rb,x0,y0,ang,nn)
% This function draws a ellipse with a long radius ra,
% and short radius rb at the center (x0,y0)
% The inputs:
% ra, rb = long & short radii of the ellipse
% x0, y0= coordinates of the ellipse center
% nn = number of drawing points
% ang = angle of the long axis, in radians
% coords(nn,1-2)= vectors to store the coordinates
% Example: ellixy(10,0,0,10)
jj=0:2*pi/nn:2*pi;
coords=[ra*cos(ang)*cos(jj)-rb*sin(ang)*sin(jj)+x0;...
ra*sin(ang)*cos(jj)+rb*cos(ang)*sin(jj)+y0];
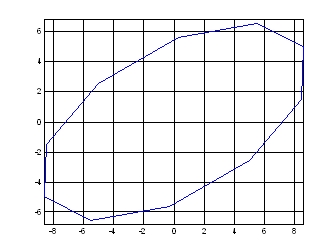 圖11.橢圓曲線之形成
圖11.橢圓曲線之形成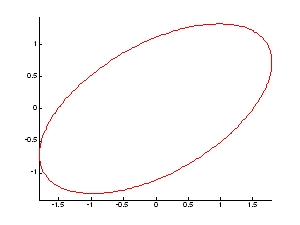 圖12 具有傾斜角度之ellipse 圓
圖12 具有傾斜角度之ellipse 圓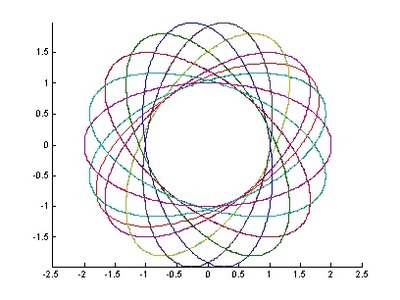 圖13.橢圓產生不同角度旋轉時之變化
圖13.橢圓產生不同角度旋轉時之變化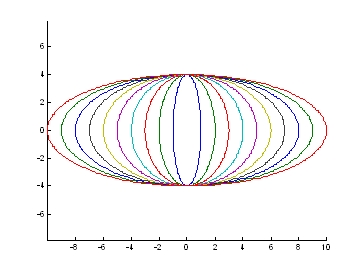 圖14.短徑不變,橢圓產生不同長徑時之變化
圖14.短徑不變,橢圓產生不同長徑時之變化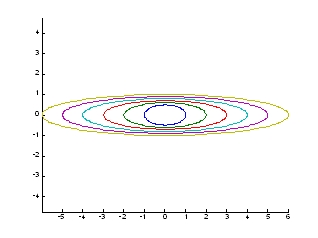 圖15.橢圓長短徑同時變化
圖15.橢圓長短徑同時變化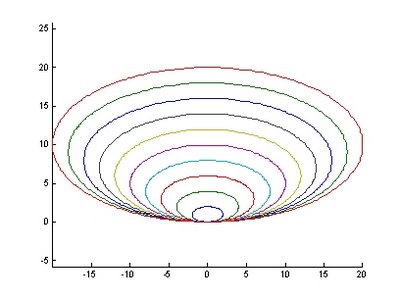 圖16.橢圓產生不同長徑時之變化
圖16.橢圓產生不同長徑時之變化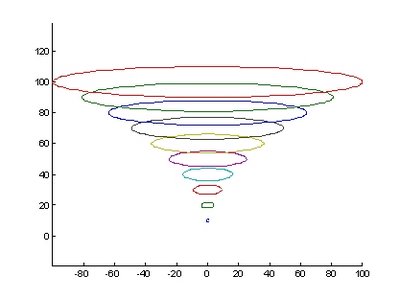 圖17.橢圓產生不同長徑時之變化
圖17.橢圓產生不同長徑時之變化
沒有留言:
張貼留言